Tableau Method

Tableau method is a method to proof satisfiability of a set of formulas.

It is also used to proof a formula to be tautology using proof by contraction.

Basic rules

• We have to break the complex formula until it gets to single atomic formulas.
• Logical $\vee$ creates branches (that’s obvious as it makes two sets out of single set).
• Each of the branch should have every formula expanded at least once.
• If there is a contraction of any atomic formula in the branch, then that branch is closed.
• If all the branches are closed then set of formulas is not satisfiable.
• If there is any one branch opened, set is satisfiable.

Info

Closed: When there is any contraction exists for any formula in a branch. Opened: Opposite of closed.

Let’s see an example for better understanding.

$set=\{(a\vee b)\wedge c,\neg b\vee \neg c,\neg a\}$

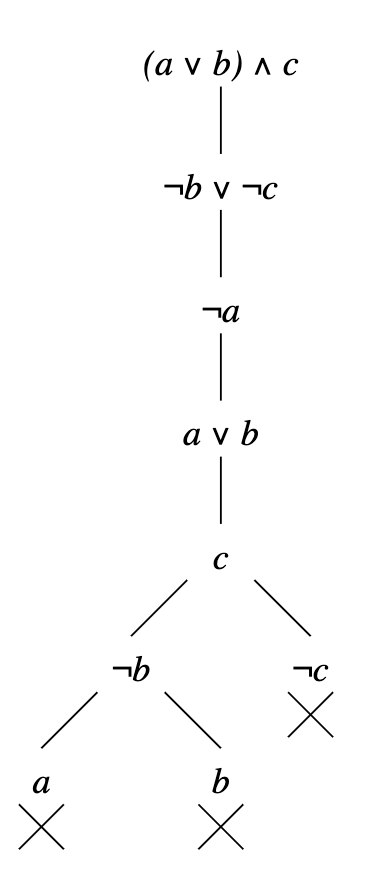
Proof Tautologies

A tautology can be proofed by taking the negate of that and try to proof satisfiability for that negate using tableau method. If that negate is unsatisfiable, then the tautology is proofed.

example, let’s proof modus ponens

$(A\wedge (A\to B))\to B$

Taking negation of this,

$\neg ((A\wedge (A\to B))\to B)$

   ~((A ∧ (A -> B)) -> B)
           |
     (A ∧ (A -> B))
           |
          ~B
           |
           A
           |
        (A -> B)
        /      \
       /        \
     ~A         B
    CLOSED    CLOSED

So, both branches are closed and there is no model for the negation. So, we can conclude that Modus Ponens is a tautology.

References

1. Propositional tableaux - DIAG